异步联邦学习
在传统的数据中心设置中,同步和异步方案都常用于并行迭代优化算法,每种方法都有优缺点。同步方案简单且保证了串行等效计算模型,但在设备变化面前,它们也更容易受到掉队者的影响。异步方案是一种很有吸引力的方法来减轻异构环境中的掉队问题。
在联邦学习中,不同平台数据分布大概率是Non-iid的,因此在该类问题中,存在不同平台计算速度不同的问题。若进行同步更新的话,即每一轮参数更新都同步,等到最慢的平台计算完成后,再同步进行参数更新,这种方法效率较低。采用异步通信的方法可以提升联邦学习或分布式机器学习的计算效率。在异步通信中,不同平台的计算速度有所不同,假设计算较快的平台已经迭代待第n次,计算较慢的平台迭代到第n-m次,惨依旧可以结合各个平台的计算结果进行非同步的参数更新。但是,在这种方法下,首先需要证明该参数更新的方式是收敛的。
1. 待解决问题
对以下问题用异步通信的方式求minimization.
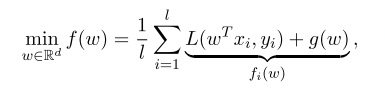
梯度计算如下:

2. 异步通信
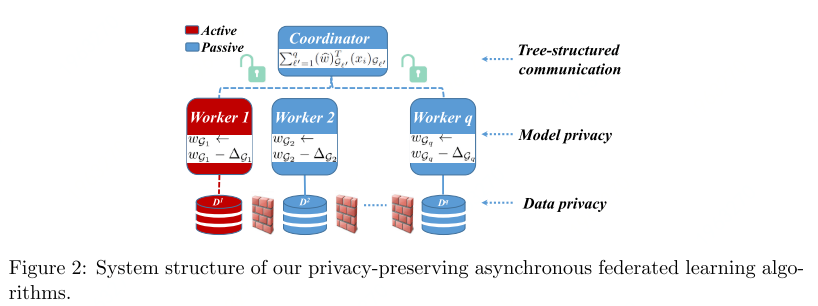
参数表示:

利用tree-structured communication scheme 计算梯度
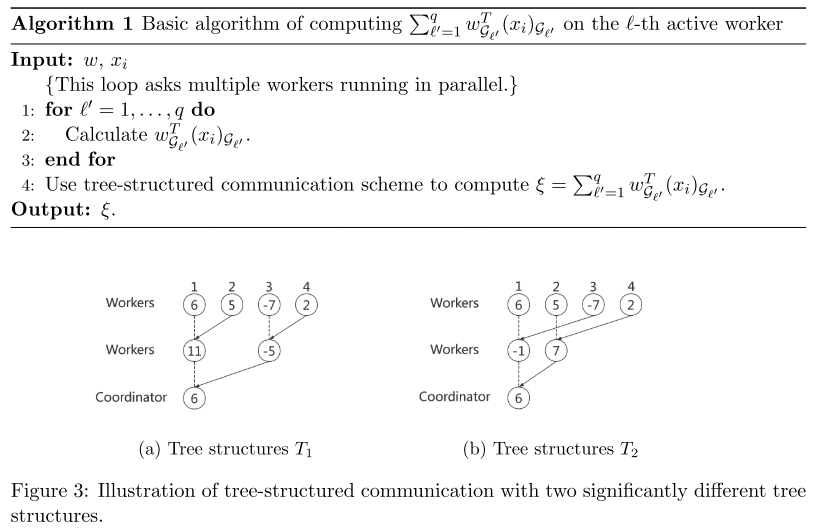
利用tree-structure T1和tree-structure T2 计算总和,以达到隐私保护的目的:

3. 梯度计算
AFSGD-VP algorithm:


Compared to AFSGD-VP, AFSVRG-VP has the following three difference:


此处相当于增加了global的参数,但不用用全部的数据集来计算Ws,每一轮有更新赋值。
AFSAG-VP:

4. 收敛性分析
convex analysis : strong convexity, smoothness, bounded gradients.

the global time counter plays a fundamental role in the convergence rate analyses. \(K(t),表示从第t个itration起,最小的迭代集合使得遍历全部的coordinates\)